열심히 살지 말자
2016년 3월 29일 화요일
Catalyst driver package ver. 15.30 has caused a crash when MATLAB called plot command
Now I use driver package ver. 16.15.
Plot command works well.
2015년 6월 21일 일요일
특이값분해(Principal Component Analysis:PCA)가 어떻게 선형 자기상관성을 제거하는가?
이 문서는 특이값분해를 알아야 이해할 수 있습니다.
직교행렬의 특징에 대해서도 알아야 합니다.
우선 PCA의 과정을 간추려보자.
행렬 A를 아래와 같이 정의해보자

각 열은 공정 하나의 데이터 혹은 데이터마이닝에서 instance내지 transaction으로 부르는 것이다. 또, 각 행은 특성, 혹은 attribute라고 부르는 것이다.
즉, 확보된 데이터가 충분히 크다면 이는 (n>m)이 되어 Thin matrix가 된다.
1) 공분산행렬을 고유값분해(Eigenvalue decomposition of covariance matrix)
여기서 P에다가 고유값분해를 시전하면
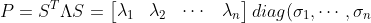\begin{bmatrix}{\lambda}_{1}\\{\lambda}_{2}\\\vdots\\{\lambda}_{n}\end{bmatrix})
가 되는데 여기서 S는 P의 고유벡터들을 가로로 눕힌것들의 집합이다.
여기서 행렬 S를 뽑는다. P는 대칭행렬이므로(공분산은 교환법칙이 성립하므로, 대칭행렬이 될수밖에 없음) S는 직교행렬이 되고, 직교행렬의 특징에따라
 or
or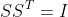
를 만족한다.
이와같은 절차로 S의 각 행을 주성분(Principal component)라고 한다.
2)데이터행렬을 특이값분해(Singular value decomposition)
특이값분해는 아래와 같다.

이며, 분해된 각 행렬들은
U:AA'의 고유벡터들을 세로로 세워둔거
Σ:A'A의 고유값들의 대각행렬을 포함하는 직사각행렬
V:A'A의 고유벡터들을 세로로 세워둔 것.
여기서 A'A의 특징을 잘 알아볼 이유가 있는데 이는 행렬의 곱연산의 정의로 보면...

이 되는데, 벡터의 내적을 n으로 나누면 공분산이 된다.(공분산의 정의 참고)
즉 A'A를 고유값분해하는 것은 P의 고유벡터인 S를 찾는것이 된다.
S=kV'
따라서 A=BS로 분해한다는 것은 A=kBV'가 되는 것이며, kB=UΣ이므로 이또한 직교행렬이 된다.
직교행렬이라는 것은 서로 다른 열끼리의 내적값이 0이라는 것이므로, 상관계수가 0이라는 뜻이다.
직교행렬의 특징에 대해서도 알아야 합니다.
우선 PCA의 과정을 간추려보자.
행렬 A를 아래와 같이 정의해보자
각 열은 공정 하나의 데이터 혹은 데이터마이닝에서 instance내지 transaction으로 부르는 것이다. 또, 각 행은 특성, 혹은 attribute라고 부르는 것이다.
즉, 확보된 데이터가 충분히 크다면 이는 (n>m)이 되어 Thin matrix가 된다.
1) 공분산행렬을 고유값분해(Eigenvalue decomposition of covariance matrix)
여기서 P에다가 고유값분해를 시전하면
가 되는데 여기서 S는 P의 고유벡터들을 가로로 눕힌것들의 집합이다.
여기서 행렬 S를 뽑는다. P는 대칭행렬이므로(공분산은 교환법칙이 성립하므로, 대칭행렬이 될수밖에 없음) S는 직교행렬이 되고, 직교행렬의 특징에따라
를 만족한다.
이와같은 절차로 S의 각 행을 주성분(Principal component)라고 한다.
2)데이터행렬을 특이값분해(Singular value decomposition)
특이값분해는 아래와 같다.
이며, 분해된 각 행렬들은
U:AA'의 고유벡터들을 세로로 세워둔거
Σ:A'A의 고유값들의 대각행렬을 포함하는 직사각행렬
V:A'A의 고유벡터들을 세로로 세워둔 것.
여기서 A'A의 특징을 잘 알아볼 이유가 있는데 이는 행렬의 곱연산의 정의로 보면...
이 되는데, 벡터의 내적을 n으로 나누면 공분산이 된다.(공분산의 정의 참고)
즉 A'A를 고유값분해하는 것은 P의 고유벡터인 S를 찾는것이 된다.
S=kV'
따라서 A=BS로 분해한다는 것은 A=kBV'가 되는 것이며, kB=UΣ이므로 이또한 직교행렬이 된다.
직교행렬이라는 것은 서로 다른 열끼리의 내적값이 0이라는 것이므로, 상관계수가 0이라는 뜻이다.
2015년 4월 14일 화요일
비선형시스템의 가관측성 (Observability of nonlinear system)
실제로 관측기를 설계할 때, 시스템이 관측가능한지 가능하지 않은지는 체크하지 않고 그냥 하는 경우가 많다. 실제로도 불가능한것보다 가능한게 더 많고.
그런데 논문쓸땐 관측가능한지 아닌지 꼭 적는것 같다. 그래서 비선형시스템의 가관측성에 대해서 글을 써봄.
우선 선형시스템부터.

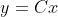
이라는 시스템이 있다고 해보자. (왜 입력이 없냐? 라고 반문할수도 있지만 이미 u는 알고있으므로 이항해서 다른변수로 치환하여 소거해도 댐)
이때 이 시스템의 거동은 y를 쭉 미분해보면 아래와 같이 나타낼 수 있다.
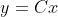
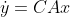
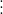
}=CA^{n-1}x)
이럴때 다시 이를 행렬을 이용한 일차 연립 상미분방정식으로 나타내면 아래와 같다.
}\end{bmatrix}=\begin{bmatrix}C\\\vdots\\CA^{(n-1)}\end{bmatrix}x)
A가 n x n 정방행렬이고 C가 1 x n 행벡터면
y는 스칼라고 x는 열벡터다. 이때
y의 거동을 결정하는 유일한 x가 존재한다 라는 명제와
}}\end{bmatrix}^{T}) 가 full column rank이다라는 명제는 동치가 된다.
가 full column rank이다라는 명제는 동치가 된다.
즉 y가 움직이고 있는 모양새를 보고 x를 추측해낼 수 있다는 얘기.
그럼 이번에 얘기하고자 하는 비선형 시스템
n크기의 열벡터 x에 대해
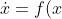)
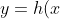)
여기서 f는 n차원 공간에서 n차원 공간으로 사상하는 함수고
h는 n차원 공간에서 1차원 공간으로 사상하는 부드러운(모든 영역에서 미분가능)한 함수다.
(내가 수식입력하는 방법으로는 왜인지 \to \rightarrow \mapsto 가 안먹힘)
이러한 시스템에다가 리 미분값(Lie derivative)을 정의해보자.
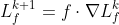
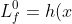)
(사실 본인생각은 표기가 깔끔한것만 빼면 내적연산자의 순서를 바꾸고싶다)
이때, 선형시스템의 y값의 거동을 나타내는 연립방정식의 형태로 나타내보자.
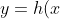=L^{0}_{f})
}=\dot{x}\frac{\partial{h}}{\partial{x}}=f\cdot\nabla{L^{0}_{f}}=L^{1}_{f})
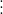
}=f\cdot\nabla{L^{(n-2)}_{f}}=L^{(n-1)}_{f})
이걸 다시 잘 정리하면
}\end{bmatrix}=\begin{bmatrix}L^{(0)}_{f}\\\cdots\\L^{(n-1)}_{f}\end{bmatrix})
여기서 이것만으론 x와의 관계를 선형연립방정식으로 나타낼수 없으니까.
안타깝지만 여기서 초기치인 x0에서의 지역적 선형화(혹은 1차까지만의 테일러급수)를 해보자. 그러면 위의 식은 아래와 같이 변형된다
}\end{bmatrix}=\begin{bmatrix}L^{(0)}_{f}\\\cdots\\L^{(n-1)}_{f}\end{bmatrix}|_{x=x_{0}}+\begin{bmatrix}\nabla{L^{(0)}_{f}}\\\cdots\\\nabla{L^{(n-1)}_{f}}\end{bmatrix}|_{x=x_{0}}(x-x_{0}))
그럼 우변에서 첫번째 항은 상수고 두번째항은 선형변환이 된다.
저 식을 이래저래 정리하여 상수항을 죄다 왼쪽에다가 몰으면 우변은
}_{f}}\\\cdots\\\nabla{L^{(n-1)}_{f}}\end{bmatrix}|_{x=x_{0}}x)
만 남게 되고 이 선형변환이 유일한 x값을 가질 수 있으면 (즉 full rank)면 이 시스템은 관측가능하다고 할 수 있다.
출처
http://www.me.berkeley.edu/ME237/6_cont_obs.pdf
그런데 논문쓸땐 관측가능한지 아닌지 꼭 적는것 같다. 그래서 비선형시스템의 가관측성에 대해서 글을 써봄.
우선 선형시스템부터.
이라는 시스템이 있다고 해보자. (왜 입력이 없냐? 라고 반문할수도 있지만 이미 u는 알고있으므로 이항해서 다른변수로 치환하여 소거해도 댐)
이때 이 시스템의 거동은 y를 쭉 미분해보면 아래와 같이 나타낼 수 있다.
이럴때 다시 이를 행렬을 이용한 일차 연립 상미분방정식으로 나타내면 아래와 같다.
A가 n x n 정방행렬이고 C가 1 x n 행벡터면
y는 스칼라고 x는 열벡터다. 이때
y의 거동을 결정하는 유일한 x가 존재한다 라는 명제와
즉 y가 움직이고 있는 모양새를 보고 x를 추측해낼 수 있다는 얘기.
그럼 이번에 얘기하고자 하는 비선형 시스템
n크기의 열벡터 x에 대해
여기서 f는 n차원 공간에서 n차원 공간으로 사상하는 함수고
h는 n차원 공간에서 1차원 공간으로 사상하는 부드러운(모든 영역에서 미분가능)한 함수다.
(내가 수식입력하는 방법으로는 왜인지 \to \rightarrow \mapsto 가 안먹힘)
이러한 시스템에다가 리 미분값(Lie derivative)을 정의해보자.
(사실 본인생각은 표기가 깔끔한것만 빼면 내적연산자의 순서를 바꾸고싶다)
이때, 선형시스템의 y값의 거동을 나타내는 연립방정식의 형태로 나타내보자.
이걸 다시 잘 정리하면
여기서 이것만으론 x와의 관계를 선형연립방정식으로 나타낼수 없으니까.
안타깝지만 여기서 초기치인 x0에서의 지역적 선형화(혹은 1차까지만의 테일러급수)를 해보자. 그러면 위의 식은 아래와 같이 변형된다
그럼 우변에서 첫번째 항은 상수고 두번째항은 선형변환이 된다.
저 식을 이래저래 정리하여 상수항을 죄다 왼쪽에다가 몰으면 우변은
만 남게 되고 이 선형변환이 유일한 x값을 가질 수 있으면 (즉 full rank)면 이 시스템은 관측가능하다고 할 수 있다.
출처
http://www.me.berkeley.edu/ME237/6_cont_obs.pdf
리아프노프 안정성 (Lyapunov stability)
오늘 읽은 글에 대해서 써봐야겠다.
출처는 영어위키
(URL: http://en.wikipedia.org/wiki/Lyapunov_stability)
영어위키의 글을 순수하게 번역하면 이렇다.
안정하다는 말은 시스템의 상태변수 가
가  근처에서 머무른다고 할때 이
근처에서 머무른다고 할때 이  는 안정하고
는 안정하고  를 안정점이라고 한다.
를 안정점이라고 한다.
1. 모든 에 대해
에 대해 -x_{e}\end{Vmatrix}<\delta) 이고 모든 양수
이고 모든 양수  에 대하여
에 대하여 -x_{e}\end{Vmatrix}<\epsilon) 를 만족하는
를 만족하는  이 존재한다면 리아프노프 안정하다고 한다.
이 존재한다면 리아프노프 안정하다고 한다.
이 말을 좀 정성적으로 바꿔보면 이렇다.
출처는 영어위키
(URL: http://en.wikipedia.org/wiki/Lyapunov_stability)
영어위키의 글을 순수하게 번역하면 이렇다.
안정하다는 말은 시스템의 상태변수
1. 모든
이 말을 좀 정성적으로 바꿔보면 이렇다.
그림의 사인함수처럼 안정점으로부터 일정 거리이상 튕겨나가지 않는 것을 리아프노프 안정하다고 하는 것이다. 또 -x_{e}\end{Vmatrix}<\delta) 의 의미는 시작지점과 안정점과의 차이가 0이 아니어도 된다는 것이다.(라고 생각한다. 다르게 생각하는 사람이 있다면 댓글로 적어주길 바란다.)
의 의미는 시작지점과 안정점과의 차이가 0이 아니어도 된다는 것이다.(라고 생각한다. 다르게 생각하는 사람이 있다면 댓글로 적어주길 바란다.)
반대로 리아프노프 안정하지 않은 시스템은?
이렇게 안정점으로부터의 거리가 무한하게 되는 경우를 말한다. (증가하는 것 뿐만 아니라 탄젠트함수처럼 중간에 무한이 되어도 리아프노프 안정하지 않다.)
- Lyapunov stability of an equilibrium means that solutions starting "close enough" to the equilibrium (within a distance
 from it) remain "close enough" forever (within a distance
from it) remain "close enough" forever (within a distance  from it). Note that this must be true for any
from it). Note that this must be true for any  that one may want to choose.
that one may want to choose.
라고 부연설명이 나오는데 직역하면 평형과 "충분히 가깝게" 출발해서 "충분히 가까운"상태에 영원히 머문다. 라고쯤...
2. -x_{e}\end{Vmatrix}<\delta) 인데
인데 -x_{e}\end{Vmatrix}) 가 0으로 수렴하면 이는 점근적으로 안정하다고 한다.
가 0으로 수렴하면 이는 점근적으로 안정하다고 한다.
그림처럼 x=0에 가까워지는걸 말한다.
- Asymptotic stability means that solutions that start close enough not only remain close enough but also eventually converge to the equilibrium.
직역은 점근적으로 안정하다는 건 "충분히 가깝게"시작하여 머무르는 것만이 아닌, 때때로 평형에 수렴하려고 하는 것만을 말한다.
3.  일때 모든
일때 모든 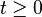 에 대하여
에 대하여  를 만족하는
를 만족하는  들이 있다면 이를 지수적으로 안정하다고 한다.
들이 있다면 이를 지수적으로 안정하다고 한다.
 일때 모든
일때 모든 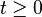 에 대하여
에 대하여  를 만족하는
를 만족하는  들이 있다면 이를 지수적으로 안정하다고 한다.
들이 있다면 이를 지수적으로 안정하다고 한다.- Exponential stability means that solutions not only converge, but in fact converge faster than or at least as fast as a particular known rate
 .
.
직역은 때때로 수렴하려고만 하는게 아니라, 최소한 특정한 목표치보다 더 빠르게 수렴한단뜻.
제어하는 사람에게 중요한건 이런 안정성의 정의보다는 리아프노프 제 2방법을 아는 것이 더 중요하다.
리아프노프 함수 V(x)를 설정하고 이 함수가 x=0외의 지점에선 Positive definite이며 그 도함수는 negative definite면 이는 점근적으로 안정하다고 볼 수 있음...
그 예시는 아래와 같음.
피드 구독하기:
덧글 (Atom)



